1. 클러스터링에 대한 소개
1.1 클러스터링의 개념과 목적
클러스터링은 비슷한 특징을 가진 데이터들을 그룹으로 묶는 비지도 학습 알고리즘입니다. 클러스터링의 목적은 유사한 데이터를 하나의 그룹으로 묶어 비슷한 특성을 갖고 있는 데이터끼리 더 잘 이해하고 분석하기 위함입니다. 클러스터링은 데이터의 패턴을 발견하고, 유사한 데이터들을 그룹으로 분류하는데 사용됩니다. 예를 들어, 고객 세분화, 이미지 분류, 소셜 미디어 분석 등 다양한 분야에서 활용됩니다.
1.2 클러스터링의 활용 분야
클러스터링은 다양한 분야에서 활용됩니다. 예를 들어, 마케팅 분야에서는 고객을 그룹으로 나누어 특정 그룹의 특성을 파악하여 정확한 마케팅 전략을 수립할 수 있습니다. 또한, 의료 분야에서는 질병 패턴을 분석하여 효과적인 치료법을 찾을 수 있습니다. 이미지 분류나 텍스트 분석에도 클러스터링이 활용되어 효율적으로 데이터를 분류할 수 있습니다.
1.3 K-Means 알고리즘 소개
K-Means 알고리즘은 가장 간단하고 널리 사용되는 클러스터링 알고리즘 중 하나입니다. K-Means 알고리즘은 클러스터링을 위해 데이터를 K개의 그룹으로 나눈다는 아이디어에 기반합니다. 알고리즘은 초기에 K개의 중심점을 랜덤하게 설정하고, 각 데이터를 가장 가까운 중심점에 할당한 다음, 할당된 데이터들의 평균을 중심으로 다시 중심점을 업데이트하는 과정을 반복합니다. 알고리즘이 수렴할 때까지 이 과정을 반복하면, 최종적으로 각 데이터가 하나의 클러스터에 소속됩니다.
다음으로 2. K-Means 알고리즘의 원리에 대해 자세히 알아보겠습니다.
2. K-Means 알고리즘의 원리
K-Means 알고리즘은 클러스터링을 위해 데이터를 K개의 그룹으로 나누는 데 사용되는 알고리즘입니다. 알고리즘은 다음과 같은 단계로 진행됩니다.
2.1 초기 중심점 설정
먼저, K개의 중심점을 초기에 랜덤하게 설정해야 합니다. 중심점은 클러스터의 대표점이며, 각 데이터가 어떤 클러스터에 속하는지 결정하는 기준이 됩니다.
2.2 데이터 점들을 가까운 중심점에 할당
각 데이터 점을 가장 가까운 중심점에 할당합니다. 데이터 점과 중심점 간의 거리를 계산하여 가장 가까운 중심점을 찾아 해당 클러스터에 할당합니다. 이 과정을 데이터 포인트의 개수만큼 반복합니다.
2.3 클러스터의 중심점 재조정
각 데이터가 할당된 후, 클러스터의 중심점을 할당된 데이터들의 평균으로 재조정합니다. 이렇게 재조정한 중심점은 클러스터를 대표하는 새로운 위치가 됩니다.
2.4 2~3과정 반복
클러스터의 중심점을 재조정한 후, 다시 데이터 점들을 가까운 중심점에 할당하는 과정과 클러스터의 중심점을 재조정하는 과정을 반복합니다. 이 과정은 더 이상 중심점이 이동하지 않을 때까지 반복되며, 알고리즘이 수렴합니다.
K-Means 알고리즘은 중심점의 초기 설정에 따라 결과가 달라질 수 있으며, 수렴 시점이 전체 데이터셋에 대해 최적의 클러스터링 결과를 보장하지는 않습니다. 따라서, 알고리즘을 실행하는 횟수를 늘려 다양한 초기 설정으로 결과를 확인하거나, 결과를 평가하여 최적의 클러스터링 결과를 선택할 수 있습니다.
이제 3. 파이썬을 이용한 K-Means 구현에 대해 알아보겠습니다.
3. 파이썬을 이용한 K-Means 구현
K-Means 알고리즘은 파이썬의 scikit-learn 라이브러리를 통해 간단하게 구현할 수 있습니다. 아래는 K-Means 알고리즘을 구현하는 방법을 설명합니다.
3.1 필요한 라이브러리 설치
K-Means 알고리즘을 구현하기 위해서는 scikit-learn 라이브러리를 설치해야 합니다. 다음 명령어를 사용하여 설치할 수 있습니다.
pip install scikit-learn3.2 데이터 전처리
K-Means 알고리즘에 사용할 데이터를 불러오고, 전처리 과정을 거쳐야 합니다. 예를 들어, CSV 파일로부터 데이터를 불러오고 필요한 형태로 변환하는 작업을 수행해야 합니다.
3.3 K-Means 알고리즘 구현
scikit-learn의 cluster 모듈에서 제공하는 KMeans 클래스를 사용하여 K-Means 알고리즘을 구현할 수 있습니다. 이 클래스는 다양한 매개변수와 메서드로 클러스터링을 수행할 수 있습니다. 일반적으로 다음과 같은 매개변수를 설정해야 합니다.
n_clusters: 클러스터의 개수를 지정합니다.init: 초기 중심점 설정 방법을 지정합니다.max_iter: 알고리즘의 최대 반복 횟수를 지정합니다.random_state: 초기 중심점 설정을 위한 시드 값을 지정합니다.
KMeans 클래스의 fit() 메서드를 호출하여 알고리즘을 실행합니다.
3.4 결과 시각화
K-Means 알고리즘의 결과를 시각화하여 확인할 수 있습니다. matplotlib 라이브러리를 사용하여 클러스터의 중심점을 표시하고 데이터 포인트를 색상별로 구분하는 작업을 수행할 수 있습니다.
이제 실제 데이터로 K-Means를 적용해보겠습니다. 4. 실제 데이터로 K-Means 적용에서 계속해서 설명하겠습니다.
4. 실제 데이터로 K-Means 적용
이제 K-Means 알고리즘을 실제 데이터에 적용해보도록 하겠습니다.
4.1 공공 데이터셋 소개
실제 데이터로는 "Iris" 데이터셋을 사용하겠습니다. Iris 데이터셋은 꽃의 품종을 분류하기 위해 유명한 데이터셋으로, 각 데이터 포인트는 꽃의 꽃잎(petal)과 꽃받침(sepal)의 길이와 너비를 나타냅니다. 이 데이터셋은 scikit-learn 라이브러리에서 제공하며, 다음과 같이 불러올 수 있습니다.
from sklearn.datasets import load_iris
iris = load_iris()
data = iris.data
target = iris.target4.2 데이터 전처리 및 시각화
전처리를 위해 필요한 패키지와 데이터를 불러온 후, 데이터를 시각화해보겠습니다. 꽃잎의 길이와 너비를 x, y 좌표로 하고, 각 데이터 포인트를 색상으로 구분하여 산점도를 그려보겠습니다.
import matplotlib.pyplot as plt
plt.scatter(data[:, 0], data[:, 1], c=target)
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.title('Iris Dataset')
plt.show()
4.3 K-Means 알고리즘 적용
데이터 전처리를 마친 후, K-Means 알고리즘을 적용해보겠습니다. 다음은 KMeans 클래스를 사용하여 K-Means 알고리즘을 적용하는 예제입니다.
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(data)
labels = kmeans.fit_predict(data)
plt.scatter(data[:, 0], data[:, 1], c=labels)
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.title('Iris Dataset')
plt.show()
4.4 클러스터 결과 해석
클러스터링 결과를 시각화하여 확인할 수 있습니다. 이를 위해 K-Means 알고리즘을 적용한 후, 클러스터에 할당된 데이터 포인트와 클러스터의 중심점을 나타내는 코드를 작성해보세요. 이를 통해 꽃의 종류에 따라 얼마나 잘 클러스터링이 되었는지 확인할 수 있습니다.
 |
 |
| 원본 | K-Means |
 |
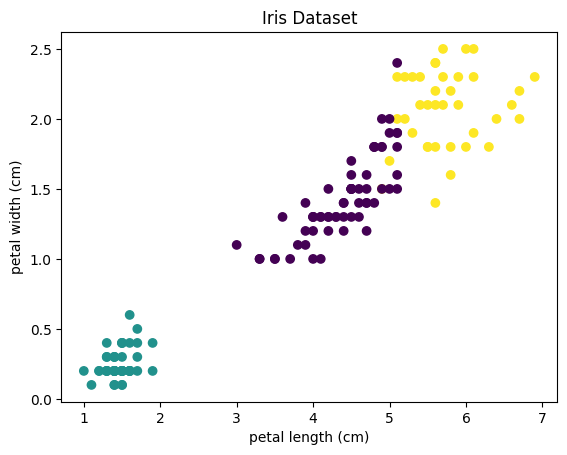 |
5. K-Means의 장단점과 확장
5.1 K-Means의 장점
- 구현이 간단하고 이해하기 쉽습니다. 초기 중심점 설정과 할당, 재조정 과정이 단순하게 반복됩니다.
- 대용량 데이터에도 적용 가능하며, 비교적 빠른 속도로 결과를 도출할 수 있습니다.
- 클러스터의 크기와 모양에서 유연성을 가지고 있습니다.
5.2 K-Means의 단점
- 초기 중심점 설정에 따라 결과가 달라지므로 초기화에 따른 불안정성이 있습니다. 잘못된 초기 중심점 설정으로 인해 원하는 결과를 얻지 못할 수 있습니다.
- 클러스터의 모양이 원형으로 가정되고, 클러스터링 결과가 원형의 형태를 갖게 됩니다. 선형적으로 구분되는 경우나 비선형적인 형태에서는 성능이 떨어질 수 있습니다.
- 이상치에 민감하게 반응하며, 이상치가 클러스터링 결과에 큰 영향을 줄 수 있습니다.
5.3 K-Means 확장 알고리즘 소개
K-Means의 단점을 보완하기 위해 여러 확장 알고리즘이 개발되었습니다. 몇 가지 대표적인 확장 알고리즘을 소개하겠습니다.
- K-Means++: 초기 중심점을 더 효과적으로 설정하기 위해 개발된 알고리즘으로, 초기화 과정에서 중심점 간의 거리를 고려하여 초기 중심점을 선택합니다.
- MiniBatch K-Means: 대용량 데이터에 대해 효율적으로 클러스터링을 수행하기 위해 개발된 알고리즘입니다. 일부 데이터의 미니배치를 사용하여 클러스터링을 수행합니다.
- DBSCAN: 밀도 기반 클러스터링 알고리즘으로, 데이터 포인트의 근접성을 기준으로 클러스터를 형성합니다. 임의의 모양의 클러스터를 찾을 수 있는 장점이 있습니다.
- Hierarchical Clustering: 계층적 클러스터링으로, 클러스터의 계층 구조를 형성합니다. 클러스터 간의 거리나 유사도를 기준으로 클러스터를 유연하게 형성할 수 있습니다.
각 확장 알고리즘은 K-Means의 한계를 극복하기 위해 특정한 상황에 적용될 수 있으며, 선택하기 전에 데이터의 특성과 목적을 고려해야 합니다.
6. 결론
K-Means 알고리즘은 간단하면서도 효과적인 클러스터링 알고리즘으로 널리 사용됩니다. 이번 글에서는 K-Means 알고리즘의 소개부터 파이썬을 이용한 구현까지 살펴보았으며, 실제 데이터로의 적용과 장단점, 그리고 확장 알고리즘들을 알아보았습니다. 클러스터링은 다양한 분야에서 유용하게 활용될 수 있으므로, 필요한 상황에 따라 적절한 알고리즘을 선택하여 활용하는 것이 중요합니다.
본 블로그 글은 G-ChatBot 서비스를 이용하여 AI(ChatGPT) 도움을 받아 작성하였습니다.
G-ChatBot
Our service is an AI chatbot service developed using OpenAI API. Our service features a user-friendly interface, efficient management of token usage, the ability to edit conversation content, and management capabilities.
gboysking.net
'ChatGPT > 인공지능' 카테고리의 다른 글
| 머신러닝이란? (0) | 2024.03.20 |
|---|---|
| [Python][ML] 스펙트럴(Spectral) 클러스터링 시각화 예시 (0) | 2023.09.24 |
| [Python][인공지능] 혼동 행렬, 정확도, 정밀도, 재현율 예시 (0) | 2023.09.23 |
| [ML] 포아송 분포 (Poisson Distribution)란? (1) | 2023.08.08 |
| [ML] 로그-정규 분포 (Log-Normal Distribution)란? (0) | 2023.08.08 |



