1. 로지스틱 함수 개요
로지스틱 함수는 딥러닝과 머신러닝에서 자주 사용되는 함수 중 하나입니다. 주로 이진 분류 문제에서 사용되며, 입력 변수의 값을 0과 1 사이로 제한하는 역할을 합니다. 로지스틱 함수는 이름 그대로 "로지스틱 (logistic)" 모양의 S자 형태를 가지고 있어서 시그모이드 함수(sigmoid function)라고도 불리기도 합니다.
로지스틱 함수는 실수 범위의 입력을 확률로 매핑하는 함수로 사용되기 때문에, 일반적으로 0과 1 사이의 값으로 출력됩니다. 이는 이진 분류 문제에서 어떠한 데이터가 어느 클래스에 속할 확률이 더 높은지를 예측하기 위해 사용됩니다.
로지스틱 함수는 다음과 같이 표현됩니다.
여기서 x는 입력 변수를 나타내며, 로지스틱 함수의 출력은 0과 1 사이의 값입니다. 로지스틱 함수의 그래프를 살펴보면, 입력 변수 x값이 음의 무한대에서 양의 무한대로 변화함에 따라 S자 형태의 곡선을 그리고 있음을 확인할 수 있습니다.
로지스틱 함수는 이번 블로그 글에서 앞으로 다루게 될 내용들에 중요한 역할을 합니다. 다음 섹션에서는 로지스틱 함수의 수식에 대해 자세히 알아보도록 하겠습니다.
2. 로지스틱 함수의 수식
로지스틱 함수의 수식은 다음과 같이 나타낼 수 있습니다.
로지스틱 함수는 입력 변수 x를 확률로 매핑하는 함수로, 입력 변수의 범위에 제한을 두어 0과 1 사이의 값으로 출력됩니다. 즉, 로지스틱 함수의 출력은 어떤 데이터가 어느 클래스에 속할 확률이 더 높은지를 나타냅니다.
로지스틱 함수의 그래프를 살펴보면, 입력 변수 x값에 따라 S자 형태의 곡선을 그리고 있음을 확인할 수 있습니다. 입력 변수 x가 음의 무한대에 가까워질수록 로지스틱 함수의 출력은 0에 가까워지고, x가 양의 무한대에 가까워질수록 출력은 1에 가까워집니다.
로지스틱 함수는 이진 분류 문제에서 특히 유용하게 사용됩니다. 예를 들어, 어떤 사람이 암에 걸릴 확률을 예측하기 위해서는 로지스틱 함수를 사용하여 입력 변수에 대한 확률 값을 계산할 수 있습니다.
로지스틱 함수의 그래프 표현을 위해 python을 사용해 계산식을 작성하고 그래프를 그려보면 다음과 같습니다.
import numpy as np
import matplotlib.pyplot as plt
def logistic_function(x):
return 1 / (1 + np.exp(-x))
x = np.linspace(-10, 10, 100)
y = logistic_function(x)
plt.plot(x, y)
plt.title("Logistic Function")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.show()위 코드를 실행하면, x값이 -10부터 10까지 변화함에 따라 로지스틱 함수의 그래프가 그려집니다.

3. 로지스틱 함수의 의미와 활용
로지스틱 함수는 입력 변수 x를 확률로 매핑하는 함수로, 이를 이용하여 다양한 의미와 활용을 가질 수 있습니다.
3.1 로지스틱 함수가 나타내는 의미
로지스틱 함수의 출력은 입력 변수가 어느 클래스에 속할 확률이 높은지를 나타냅니다. 로지스틱 함수는 이진 분류 문제에서 특히 유용하게 사용됩니다. 예를 들어, 병에 걸린 사람인지 아닌지를 예측하는 분류 모델을 만든다고 가정해봅시다. 로지스틱 함수를 이용하면 어떤 데이터가 양성 클래스(병에 걸린 사람)에 속할 확률과 음성 클래스(병에 걸리지 않은 사람)에 속할 확률을 계산할 수 있습니다. 따라서, 로지스틱 함수를 통해 양성 클래스에 속할 확률이 0.5를 넘는지 아닌지를 기준으로 분류를 결정할 수 있습니다.
3.2 로지스틱 함수의 활용 예시
로지스틱 함수는 다양한 분야에서 활용될 수 있습니다. 몇 가지 예시를 살펴보면 다음과 같습니다.
- 의학 분야: 암 진단, 질병 예측 등에 사용될 수 있습니다. 로지스틱 함수를 이용하여 어떤 환자가 특정 질병에 걸릴 확률을 예측할 수 있습니다.
- 마케팅 분야: 고객의 구매 확률을 예측하기 위해 사용될 수 있습니다. 로지스틱 함수를 이용하여 고객이 특정 상품을 구매할 확률을 예측할 수 있습니다.
- 금융 분야: 대출 상환 여부를 예측하기 위해 사용될 수 있습니다. 로지스틱 함수를 이용하여 고객이 대출 상환을 할 확률을 예측할 수 있습니다.
로지스틱 함수는 이진 분류 문제뿐만 아니라, 다중 클래스 분류 문제에서도 사용될 수 있습니다. 이에 대해서는 다음 섹션에서 더 자세히 다루도록 하겠습니다.
4. 로지스틱 함수의 파라미터 추정
로지스틱 함수의 파라미터 추정은 분류 모델을 학습시키는 과정 중에 필요한 단계입니다. 파라미터를 추정하는 방법에는 여러 가지가 있지만, 가장 일반적인 방법은 최대 가능도 추정 (Maximum Likelihood Estimation, MLE)입니다.
4.1 로지스틱 함수의 파라미터 추정 방법
로지스틱 함수의 파라미터인 가중치 (weight)와 편향 (bias)는 주어진 입력 데이터와 이에 대한 목표값을 비교하여 조정됩니다. 최대 가능도 추정은 주어진 데이터에서 관측된 결과를 가장 잘 설명하는 모델 파라미터를 찾는 방법입니다. 이를 위해 로그 우도 함수를 최대화하는 파라미터를 찾는 것이 핵심입니다.
로지스틱 함수에서 주로 사용되는 로그 우도 함수는 다음과 같이 정의됩니다.
여기서,
- (L(w))는 로그 우도 함수입니다.
- (N)은 데이터의 개수입니다.
- (y_i)는 실제 레이블이며, 0 또는 1의 값을 가집니다.
- (p_i)는 로지스틱 함수의 출력 값으로, (sigma(w^T x_i))로 표현됩니다.
- (w)는 가중치 벡터입니다.
- (x_i)는 입력 변수의 벡터입니다.
로그 우도 함수는 데이터의 각 샘플에 대한 예측값과 실제값의 비교를 통해 파라미터를 조정하는 데 사용됩니다. 이를 통해 데이터를 잘 설명하는 모델 파라미터를 찾을 수 있습니다.
위의 식에서 첫 번째 항은 실제 값이 1일 때, 즉 양성 클래스일 때의 예측값의 로그를 취한 것을 의미합니다. 두 번째 항은 실제 값이 0일 때, 즉 음성 클래스일 때의 예측값(1에서 뺀 값)의 로그를 취한 것을 의미합니다. 이를 모든 데이터 샘플에 대해 합산한 것이 로그 우도 함수입니다.
로지스틱 회귀 모델을 학습하는 과정에서 최대 가능도 추정을 이용하여 로그 우도 함수를 최대화하는 파라미터를 찾게 됩니다. 이를 통해 로지스틱 함수의 파라미터를 추정할 수 있습니다.
설명을 간단히 하기 위해 별다른 수학적 증명은 생략하였으니, 실제로는 이러한 수학적 원리를 기반으로 최적화 알고리즘을 사용하여 로그 우도 함수를 최대화하는 파라미터를 찾게 됩니다.
4.2 예제를 통한 파라미터 추정 실습
다음은 파이썬의 scikit-learn 라이브러리를 사용하여 로지스틱 함수의 파라미터를 추정하는 간단한 예제 코드입니다.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
# 데이터 로드
iris = load_iris()
X = iris.data
y = iris.target
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 로지스틱 회귀 모델 학습
model = LogisticRegression()
model.fit(X_train, y_train)
# 학습된 파라미터 출력
print("Estimated Coefficients: ", model.coef_)
print("Estimated Intercepts: ", model.intercept_)위 예제에서는 iris 데이터셋을 사용하여 로지스틱 회귀 모델을 학습한 후, 학습된 파라미터를 출력하고 있습니다. model.coef_는 가중치 벡터를 나타내며, model.intercept_는 편향을 나타냅니다.

5. 로지스틱 함수의 분류 문제에의 적용
로지스틱 함수는 주로 이진 분류 문제에 적용되는데, 이진 분류란 결과가 두 가지로 분류되는 문제를 말합니다. 예를 들면, 스팸 메일을 분류하는 문제나 양성/음성 판단을 하는 문제입니다. 이런 문제에서 로지스틱 함수는 확률 값을 출력하여 각 클래스에 속할 확률을 예측하는데 사용됩니다.
5.1 로지스틱 함수를 이용한 이진 분류 문제 해결
로지스틱 함수의 출력 범위는 0부터 1까지입니다. 이를 확률로 해석하면, 0에 가까울수록 음성 클래스에 속할 확률이 높고, 1에 가까울수록 양성 클래스에 속할 확률이 높습니다. 이때, 모델의 결정 경계 (decision boundary)는 로지스틱 함수가 0.5를 넘거나 같을 때, 양성 클래스로 분류하며, 그보다 작을 때 음성 클래스로 분류합니다.
로지스틱 함수를 이용해 이진 분류를 수행하는 과정은 다음과 같습니다.
- 훈련 데이터를 로지스틱 회귀 모델에 학습시킵니다.
- 학습된 모델로부터 입력 데이터에 대한 예측 확률을 계산합니다.
- 예측 확률이 임계값 (일반적으로 0.5) 이상이면 양성 클래스로 분류하고, 그렇지 않으면 음성 클래스로 분류합니다.
5.2 예제를 통한 분류 문제 실습
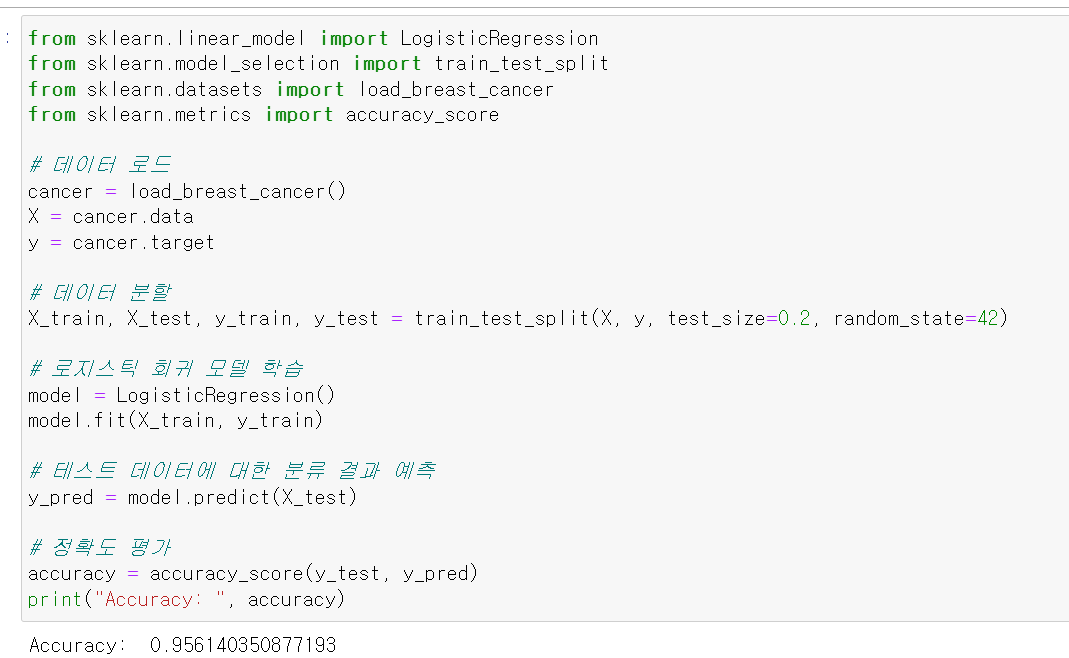
다음은 파이썬의 scikit-learn 라이브러리를 사용하여 로지스틱 회귀를 이용한 이진 분류 문제를 해결하는 간단한 예제 코드입니다.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
from sklearn.metrics import accuracy_score
# 데이터 로드
cancer = load_breast_cancer()
X = cancer.data
y = cancer.target
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 로지스틱 회귀 모델 학습
model = LogisticRegression()
model.fit(X_train, y_train)
# 테스트 데이터에 대한 분류 결과 예측
y_pred = model.predict(X_test)
# 정확도 평가
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy: ", accuracy)위 예제에서는 유방암 데이터셋을 로드한 후, 학습 데이터와 테스트 데이터로 분할합니다. 그리고 로지스틱 회귀 모델을 학습시킨 다음, 테스트 데이터에 대한 분류 결과를 예측하여 정확도를 평가하고 있습니다. accuracy_score 함수를 사용하여 예측 결과와 실제 결과를 비교하여 정확도를 계산합니다.
6. 로지스틱 함수의 확장
로지스틱 함수는 주로 이진 분류 문제에 적용되지만, 다중 클래스 분류 문제에도 확장하여 사용할 수 있습니다. 이를 위해 소프트맥스 함수 (Softmax function)를 이용하여 로지스틱 함수를 다중 클래스로 확장한 다중 로지스틱 회귀를 사용합니다.
6.1 로지스틱 함수의 다중 클래스 분류 확장
다중 클래스 분류는 세 개 이상의 클래스로 분류되는 문제를 말합니다. 로지스틱 함수의 다중 클래스 분류 확장은 여러 개의 이진 분류 문제로 변환하여 해결합니다. 이때, 소프트맥스 함수는 다중 클래스의 확률을 출력할 수 있도록 로지스틱 함수를 변형한 함수입니다.
다중 로지스틱 회귀는 다음과 같은 과정으로 이루어집니다.
- 각 클래스에 대해 이진 분류 모델을 학습시킵니다. 각 이진 분류 모델은 해당 클래스에 속할 확률을 예측하기 위한 로지스틱 함수를 사용합니다.
- 소프트맥스 함수를 이용하여 각 클래스 별 예측 확률을 계산합니다.
- 가장 높은 확률을 가지는 클래스로 데이터를 분류합니다.
6.2 다중 클래스 분류 문제 해결을 위한 로지스틱 함수 확장 예시
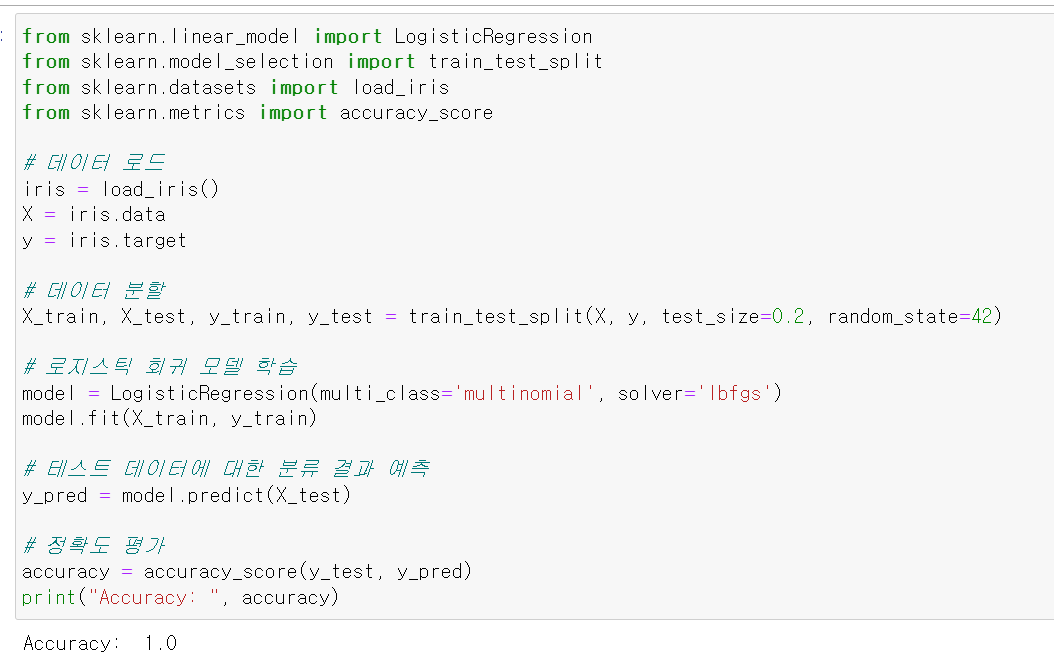
아래 예제는 scikit-learn 라이브러리를 사용하여 소프트맥스 함수를 적용한 다중 로지스틱 회귀를 사용하여 붓꽃 데이터셋을 분류하는 예제 코드입니다.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score
# 데이터 로드
iris = load_iris()
X = iris.data
y = iris.target
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 로지스틱 회귀 모델 학습
model = LogisticRegression(multi_class='multinomial', solver='lbfgs')
model.fit(X_train, y_train)
# 테스트 데이터에 대한 분류 결과 예측
y_pred = model.predict(X_test)
# 정확도 평가
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy: ", accuracy)위 예제에서는 붓꽃 데이터셋을 로드한 후, 학습 데이터와 테스트 데이터로 분할합니다. 그리고 multi_class='multinomial'과 solver='lbfgs' 옵션을 설정하여 다중 로지스틱 회귀 모델을 학습시킵니다. 마지막으로 테스트 데이터에 대한 분류 결과를 예측하고 정확도를 평가합니다.
이처럼 로지스틱 함수는 다중 클래스 분류 문제에서도 확장하여 사용될 수 있으며, 소프트맥스 함수를 이용하여 각 클래스 별 확률을 예측합니다. 다중 클래스 분류를 위한 로지스틱 회귀를 사용하면 보다 다양한 분류 문제를 해결할 수 있습니다.
본 블로그 글은 G-ChatBot 서비스를 이용하여 AI(ChatGPT) 도움을 받아 작성하였습니다.
G-ChatBot
Our service is an AI chatbot service developed using OpenAI API. Our service features a user-friendly interface, efficient management of token usage, the ability to edit conversation content, and management capabilities.
gboysking.net
'ChatGPT > 인공지능' 카테고리의 다른 글
| [ML] 로그-정규 분포 (Log-Normal Distribution)란? (0) | 2023.08.08 |
|---|---|
| [ML] 소프트맥스 함수 (Softmax Function)란? (0) | 2023.08.06 |
| [ML] 지수 분포 (Exponential Distribution)란? (0) | 2023.08.06 |
| [ML] 감마 분포 (Gamma Distribution)란? (0) | 2023.08.06 |
| [ML] 베타 분포 (Beta Distribution)란? (0) | 2023.07.30 |



